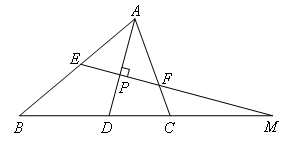
如图，在△ABC中，AD平分∠BAC，EF⊥AD于点P，交BC的延长线于点M．若∠ACB=70°，∠B=40°，则∠M的度数为(    )

如图，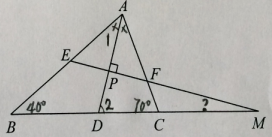

∠M可以放在Rt△DPM中，利用直角三角形两锐角互余计算，
那么需要求∠2的度数；
∠2可以看作△ABD的一个外角，
根据三角形的一个外角等于和它不相邻的两个内角的和，
得∠2=∠B+∠1，因此问题转化为求∠1的度数．
在△ABC中，∠ACB=70°，∠B=40°，
根据三角形的内角和等于180°，得∠BAC=180°-∠B-∠ACB=70°；
又因为AD平分∠BAC，根据角平分线的定义，得∠1=∠BAC=35°，
从而可以求出∠2=75°，所以∠M=90°-∠2=15°．
故选B．

略