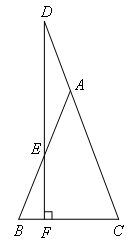
如图，在△ABC中，∠B=∠C，D为CA延长线上一点，DF⊥BC于点F，交AB于点E．求证：∠D=∠AED．

证明：如图，


                           
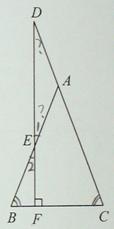
∵∠1=∠2（对顶角相等）
∴∠1=∠D（等量代换）
即∠D=∠AED
横线处应填写的过程最恰当的是(    )

• A.
  ∵DF⊥BC（已知）
  ∴∠EFB=∠DFC=90°（垂直的定义）
  ∴∠D+∠C=90°，∠2+∠B=90°（直角三角形两锐角互余）
  ∵∠B=∠C（已知）
  ∴∠2=∠D（等角的余角相等）
• B.
  ∵DF⊥BC（已知）
  ∴∠EFB=∠DFC=90°（垂直的定义）
  ∵∠B=∠C（已知）
  ∴∠D+∠C=90°，∠2+∠B=90°（直角三角形两锐角互余）
  ∴∠2=∠D（等角的余角相等）
• C.
  ∵DF⊥BC（已知）
  ∴∠EFB=∠DFC=90°（垂直的定义）
  ∴∠D+∠C=90°，∠2+∠B=90°（直角三角形两锐角互余）
  ∴∠2=∠D（等角的余角相等）
• D.
  ∵DF⊥BC（已知）
  ∴∠EFB=∠DFC=90°（垂直的定义）
  ∴∠D+∠C=90°，∠2+∠B=90°（直角三角形两锐角互余）
  ∴∠D+∠B=90°，∠2+∠C=90°（等量代换）

答案

正确答案：A

知识点：直角三角形两锐角互余  同角或等角的余角相等  垂直的定义  

第一步：读题标注（见证明过程中图形）；
第二步：走通思路，从条件出发，看到垂直怎么想？
从条件出发，看到垂直想互余．
由DF⊥BC，利用垂直的定义，得∠EFB=∠DFC=90°，
根据直角三角形两锐角互余，得到∠D+∠C=90°，∠2+∠B=90°；
又结合已知∠B=∠C，利用等角的余角相等，得∠2=∠D，
又因为∠1=∠2，等量代换，得∠1=∠D．
第三步：规划过程；
根据分析，过程主要分为三个书写模块：
①利用直角三角形两锐角互余，得到∠D+∠C=90°，∠2+∠B=90°；
②结合已知∠B=∠C，利用等角的余角相等，得到∠2=∠D；
③最后利用对顶角相等∠1=∠2，等量代换，得∠D=∠AED．
故选A．

略

下载次数：3

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>