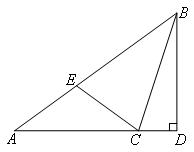
如图，点E为△ABC边AB上一点，AC=BC=BE，AE=EC，BD⊥AC于D，则∠CBD的度数为(    )

设∠A=x
∵AC=BC，AE=EC
∴∠ABC=∠A=x，∠ACE=∠A=x
∴∠BEC=∠A+∠ACE=2x
∵BC=BE
∴∠BEC=∠BCE=2x
在△BEC中，∠BEC+∠BCE+∠EBC=180°
∴2x+2x+x=180°
解得：x=36°
∴∠A=∠ABC=36°
∵BD⊥AC
∴∠D=90°
∴∠ABD=90°-∠A=54°
∴∠CBD=∠ABD-∠ABC=18°．
故选B

略