如图,将等腰三角形ABC沿DE折叠,使顶角顶点A落在两底角平分线的交点F处.
若BF=DF,则∠C的度数是( )
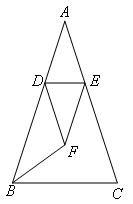
- A.80°
- B.75°
- C.72°
- D.60°
答案
正确答案:C
知识点:角平分线的定义 轴对称的应用—折叠问题
提示:三角形的三条角平分线交于一点,任意两个内角平分线的交点
一定在第三个内角的平分线上.
如图,连接CF,AF.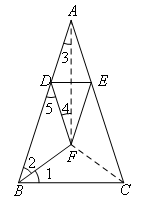
由题意知:∠ABC=∠ACB
∵点F是底角平分线的交点
∴AF平分∠BAC
设∠1=∠2=α,则∠ACB=∠ABC=2α
∴∠BAC=180°-4α
∴∠3=90°-2α
由折叠的性质可知,AD=DF
∴∠3=∠4=90°-2α
∴∠5=∠3+∠4=180°-4α
∵BF=DF
∴∠2=∠5
即α=180°-4α,解得,α=36°,
∴∠ACB=2α=72°.
故选C
略








