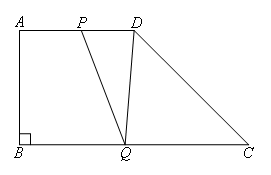
已知：如图，在梯形ABCD中，AD∥BC，∠ABC=90°，AD=12，BC=24，动点P从点A出发以每秒1个单位长度的速度沿AD方向向点D运动，动点Q从点C出发以每秒2个单位长度的速度沿CB方向向点B运动，P，Q同时出发，当点P停止运动时，点Q也随之停止，连接PQ，DQ．设点P的运动时间为t秒，当t为(    )时，△PDQ≌△CQD.

• A.12
• B.8
• C.6
• D.4

答案

正确答案：D

知识点：全等三角形  动点问题  

①研究背景图形，动点的运动状态
背景图形是一个直角梯形，且AD=12，BC=24，
由动点运动状态可知：．
②分析状态转折点，分段
此题中不涉及状态转折，所以跳过此步．
③画出符合题意的图形，表达线段长，建等式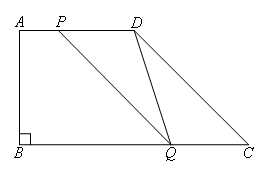

由题意得AP=t，CQ=2t
∵AD=12
∴DP=12-t
要使△PDQ≌△CQD，则需DP=QC
即12-t=2t，t=4（符合题意）
∴当t=4时，△PDQ≌△CQD．
故选D

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>