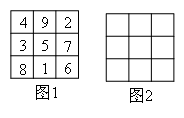
在下图的3×3的阵列中填入了1～9的自然数，构成了大家熟悉的三阶幻方．现在另有一个3×3的阵列，请选择九个不同的自然数填入九个方格中，使得每行、每列、每条对角线上的三个数之和都等于27，则正中间的方格中填写的数字应该是( )
- A.13
- B.9
- C.5
- D.7
答案
正确答案：B
知识点：三阶幻方
由于三阶幻方每行、每列、每条对角线上的三个数之和都相等，
所以三阶幻方每行、每列、每条对角线上的三个数之和是正中间数字的3倍，
要使得图2每行、每列、每条对角线上的三个数之和都等于27，
则图2中正中间的数字为27÷3=9．
故选B．
略
WORD格式（
