已知:如图,在△ABC中,CD平分∠ACB,DE∥AC,EF∥CD.
求证:∠1=∠2.
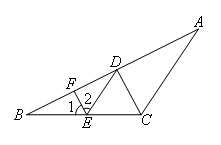
证明:如图,
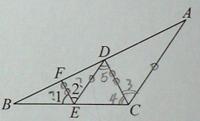
∵CD平分∠ACB(已知)
∴∠3=∠4(角平分线的定义)
∵DE∥AC(已知)
∴∠3= (两直线平行,内错角相等)
∴∠4=∠5(等量代换)
∵EF∥CD(已知)
∴∠1= (两直线平行,同位角相等)
∠5= (两直线平行,内错角相等)
∴∠1=∠2(等量代换)
①∠1;②∠2;③∠3;④∠4;⑤∠5.
以上空缺处依次所填正确的是( )
- A.⑤④①
- B.②③①
- C.⑤④②
- D.②①③
答案
正确答案:C
第一个空:条件是DE∥AC,由条件得到结论的理由是两直线平行,内错角相等,∠3和∠5是直线DE和直线AC被直线CD所截得到的内错角,因此结论应该是∠3=∠5,第一个空填⑤∠5;
第二个空:条件是EF∥CD,由条件得到结论的理由是两直线平行,同位角相等,∠1和∠4是直线EF和直线CD被直线BC所截得到的同位角,因此结论是∠1=∠4,第二个空填④∠4;
第三个空:条件是EF∥CD,由条件得到结论的理由是两直线平行,内错角相等,∠5和∠2是直线EF和直线CD被直线DE所截得到的内错角,因此结论是∠5=∠2,第三个空填②∠2.
故选C.
略









