已知:如图,点B,E,F,C在同一直线上,AB=DC,BE=CF,∠B=∠C.
求证:OA=OD.
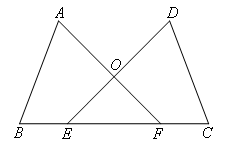
证明:如图,
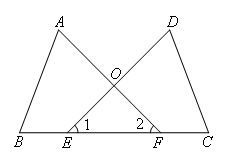
∵BE=CF
∴BE+EF=CF+EF
即BF=CE
在△ABF和△DCE中
∴△ABF≌△DCE( )
∴
∴OF=OE(等角对等边)
∴AF-OF=DE-OE
即OA=OD
请你仔细观察下列序号所代表的内容:
①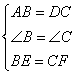 ;②
;②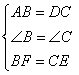 ;③SAS;④SSA;
;③SAS;④SSA;
⑤∠A=∠D,AF=DE;⑥∠1=∠2,AF=DE;⑦∠1=∠2,∠A=∠D.
以上空缺处依次所填最恰当的是( )
- A.②③⑥
- B.①③⑥
- C.②④⑦
- D.①③⑤
答案
正确答案:A
知识点:全等三角形的性质 全等三角形的判定 全等三角形证明过程训练
观察图形,题中已知AB=DC,BE=CF,∠B=∠C,
由BE=CF可得BF=CE,
可以证得△ABF≌△DCE(SAS),
得到∠1=∠2,AF=DE;
由∠1=∠2,利用等角对等边可以证得OF=OE,
因此AF-OF=DE-OE,即OA=OD.
故选A.
略









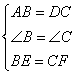 ;②
;②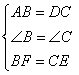 ;③SAS;④SSA;
;③SAS;④SSA;