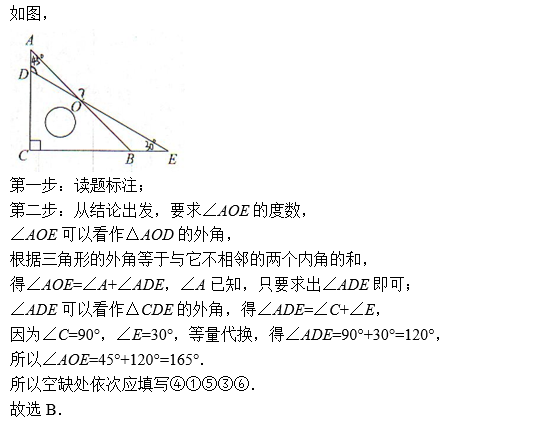
已知：如图，把一副三角板按如图方式放置，∠C=90°，∠A=45°，∠E=30°，求两条斜边相交所成的钝角∠AOE的度数．

解：如图，
∵∠ADE是△CDE的一个外角（外角的定义）
∴∠ADE=∠C+∠E（三角形的外角等于与它不相邻的两个内角的和）
∵∠C=90°，∠E=30°（已知）
                            
①∵∠AOE是△AOD的一个外角（外角的定义）
②∵∠AOE=∠A+∠ADE（外角的定义）
③∵∠A=45°（已知）
④∴∠ADE=90°+30°=120°（等量代换）
⑤∴∠AOE=∠A+∠ADE（三角形的外角等于与它不相邻的两个内角的和）
⑥∴∠AOE=45°+120°=165°（等量代换）
横线处应填写的过程，顺序正确的是(    )

• A.②④⑤⑥
• B.④①⑤③⑥
• C.④②③⑥
• D.①④③⑤

答案

正确答案：B

知识点：三角形的外角  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>