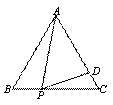
如图,在等边△ABC中,P为BC边上一点,D为AC边上一点,且∠APB+∠DPC=120°,BP=3,CD=2,则△ABC的边长为()
- A.9
- B.12
- C.16
- D.18
答案
正确答案:A
知识点:相似三角形的判定与性质
通过读题发现所有条件都集中在△ABP与△PCD中,而且由∠APB+∠DPC=120°可知,∠APD=60°,图中出现了双垂直相似模型的变形,及△ABP∽△PCD,根据对应边成比例即可求得AB的长,也就是△ABC的边长.
略




正确答案:A
知识点:相似三角形的判定与性质
通过读题发现所有条件都集中在△ABP与△PCD中,而且由∠APB+∠DPC=120°可知,∠APD=60°,图中出现了双垂直相似模型的变形,及△ABP∽△PCD,根据对应边成比例即可求得AB的长,也就是△ABC的边长.
略
