（上接第1题）（2）如图2，若∠BCA=60°，α=120°，结论EF=BE-AF仍成立吗？若成立，请给出证明，若不成立，请说明理由.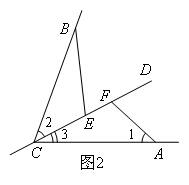

先在图上走通思路后再填写空格内容：
（2）由∠BCA=60°，∠AFC=120°，可以得到∠2+∠3=60°，∠3+∠1=60°，得到             ，理由是                      ．又因为CB=AC，∠BEC=∠CFA，因此根据全等三角形的判定           ，可以得到           ，由全等的性质得CE=AF，BE=CF，所以EF=CF-CE=BE-AF．
①∠2=∠3；②∠2=∠1；③等式性质；④同角或等角的余角相等；
⑤△BEC≌△AFC；⑥△BEC≌△CFA；⑦ASA；⑧AAS．
以上空缺处依次所填最恰当的是(    )

如图1，直线CD经过∠BCA的顶点C，点E，F在直线CD上，已知CA=CB，∠BEC=∠CFA=α．
（1）如图1，若∠BCA=90°，α=90°，试求证：EF=BE-AF．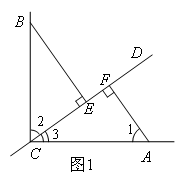

先在图上走通思路后再填写空格内容：
（1）由∠BCA=∠CFA=90°，可以得到∠2+∠3=90°，∠3+∠1=90°，得到             ，理由是                      ．
又因为BC=CA，∠BEC=∠CFA，因此根据三角形全等的判定           ，可以得到△BEC≌△CFA，由全等的性质得                      ，所以EF=CF-CE=BE-AF．
①∠2=∠1；②∠2=∠3；③同角或等角的余角相等；④同角或等角的补角相等；
⑤CE=AF，BE=AC；⑥CE=AF，BE=CF；⑦AAS；⑧ASA；
以上空缺处依次所填最恰当的是(    )

（上接第4，5题）（3）如图，当点D在边CB的延长线上时，其他条件不变，则BC，
CF，CD之间的数量关系和证明的思路分别是(    )

（上接第4题）（2）如图，当点D在边BC的延长线上时，其他条件不变，则BC，CF，CD之间的数量关系和证明的思路分别是(    )

已知△ABC中，AB=AC，点D为直线BC上一动点（不与点B，C重合），以AD为边作△ADF（A，D，F按顺时针排列），使AD=AF，且∠BAC=∠DAF，连接CF．
（1）如图，当点D在边BC上时，求证：BC=CF＋CD．

解题思路：（1）由∠BAC=∠DAF，得∠BAD=∠CAF；又因为AB=AC，AD=AF，因此根据三角形全等的判定           ，可以得到           ，由全等的性质得到                      ，通过等量代换可得BC=CF+CD．
①ASA；②SAS；③SSA；④△ADB≌△AFC；⑤△AFC≌△BAD；⑥△ADB≌△FCD；⑦BD=CF；
⑧BD=CF，BC=AC．
以上横线处依次所填最恰当的是(    )

（上接第1，2题）如图3，若以△ABC的边AB，AC为直角边向内作等腰直角△ABE和
等腰直角△ACD，其他条件不变，结论DE=2AM依然成立，如图3-1，证明的方法是延长AM到F，使MF=AM，
连接BF．先证明△BFM≌△CAM，再证明△ABF≌△EAD．证明△ABF≌△EAD时找的三组条件是(    )

（上接第1题）如图2，当△ABC为一般三角形时，DE=2AM是否依然成立？若成立写出证明DE=2AM的思路；若不成立，说明理由．下列各项正确的是(    )

以△ABC的边AB，AC为直角边向外作等腰直角△ABE和等腰直角△ACD，AB=AE，AC=AD，∠BAE=∠CAD=90°，M是BC中点，连接AM，DE．
（1）如图1，在△ABC中，当∠BAC=90°时，求AM与DE的数量关系．根据图1-1的辅助线，下面给出了解题的路线图：


①延长AM到F，使MF=AM，连接BF；②延长AM到F，使AM=MF；③延长AM到F，连接BF；
④BF=AC=AD，BF∥AC；⑤BM=CM；⑥△AFB≌△EAD（ASA）；⑦△ABF≌△EAD（SAS）．
以上横线处，依次所填最恰当的是(    )

（上接第4题）（2）如图2所示，当直线与直线MA不垂直，且交点D，E在AB的异侧时，则线段AD，BE，AB之间的数量关系和证明思路正确的是(    )

如图1，直线AM∥BN，∠MAB与∠NBA的平分线交于点C，过点C作一条直线与两条直线
MA，NB分别相交于点D，E．
（1）如图1所示，当直线与直线MA垂直时，求证：AB=AD+BE．

下面给出了证明的路线图，如图：

请你仔细观察下列序号所代表的内容：
①∠CEB=90°，∠1=∠3；②AB=BF；③AC=CF；④AB=BF，AD=EF；⑤△ACB≌△FCB（SAS）；
⑥△ADC≌△FEC（ASA）．
以上横线处，依次所填最恰当的是(    )