1编号:138059题型:解答题测试正确率:0%
(2021广安)如图,在平面直角坐标系中,抛物线y=-x2+bx+c的图象与坐标轴相交于A,B,C三点,其中点A的坐标为(3,0),点B的坐标为(-1,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒![]() 个单位长度的速度向点C做匀速运动;同时,动点Q从点B出发,在线段BA上以每秒1个单位长度的速度向点A做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接PQ,设运动时间为t秒.
个单位长度的速度向点C做匀速运动;同时,动点Q从点B出发,在线段BA上以每秒1个单位长度的速度向点A做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接PQ,设运动时间为t秒.
(1)求b,c的值.
(2)在P,Q运动的过程中,当t为何值时,四边形BCPQ的面积最小,最小值为多少?
(3)在线段AC上方的抛物线上是否存在点M,使△MPQ是以点P为直角顶点的等腰直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.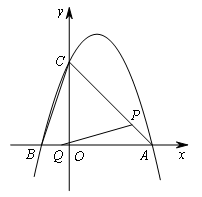
2编号:136950题型:解答题测试正确率:0%
探索发现
如图1,是一张直角三角形纸片,∠B=90°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE,EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
拓展应用
如图2,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P,N分别在边AB,AC上,顶点Q,M在边BC上,则矩形PQMN面积的最大值为 (用含a,h的代数式表示).
灵活应用
如图3,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
实际应用
如图4,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M,N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M,N在边BC上且面积最大的矩形PQMN,求该矩形的面积.