1编号:116738题型:解答题测试正确率:0%
2编号:116737题型:解答题测试正确率:0%
我们定义:如图1,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′.
当α+β=180°时,我们称△AB′C′是△ABC的“旋补三角形”,△AB′C′边B′C′上的中线AD叫做
△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2、图3中,△AB′C′是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD的长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.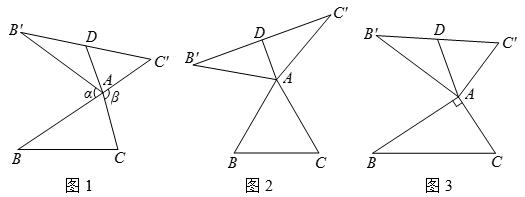
拓展应用
(3)如图4,四边形ABCD,∠C=90°,∠D=150°,BC=12,CD=![]() ,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,请给予证明,并求△PAB的“旋补中线”长;若不存在,请说明理由.
,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,请给予证明,并求△PAB的“旋补中线”长;若不存在,请说明理由.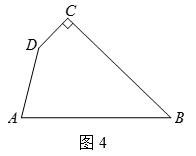
3编号:116736题型:解答题测试正确率:0%
5编号:116329题型:解答题测试正确率:0%
6编号:116306题型:解答题测试正确率:0%