（上接第3题）（3）中△DEM与△CEN的周长之和为(    )

问题情境：
张老师给爱好学习的小军和小俊提出这样一个问题：如图1，在△ABC中，AB=AC，P为BC边上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．

小军的证明思路是：如图2，连接AP，由△ABP与△ACP的面积之和等于△ABC的面积可以证得：
PD+PE=CF．
小俊的证明思路是：如图2，过点P作PG⊥CF，垂足为G，可以证得：PD=GF，PE=CG，则PD+PE=CF．
（1）变式探究：如图3，当点P在BC的延长线上时，其他条件不变，求证：PD-PE=CF；
（2）结论运用：如图4，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点处，点P为折痕EF上的任一点，过点P作PG⊥BE，PH⊥BC，垂足分别为G，H，若AD=8，CF=3，求PG+PH的值；
（3）迁移拓展：图5是一个航模的截面示意图，已知在四边形ABCD中，E为AB边上的一点，ED⊥AD，
EC⊥CB，垂足分别为D，C，且，．M，N分别为
AE，BE的中点，连接DM，CN，求△DEM与△CEN的周长之和．

（2）中PG+PH的值为(    )

（上接第3，4题）（3）中的值为(    )

（上接第3题）（2）中的值为(    )

如图1，D是△ABC的边BC上一点，过点D的一条直线交AC于点F，交BA的延长线于点E．

（1）若BD=CD，CF=2AF，请直接写出的值．
（2）如图2，若BD=CD，CF=mAF，求的值．（用含m的代数式表示）
（3）如图3，将原题改为“过点D的一条直线交AC的延长线于点F，交AB于点E，若BD=nCD，CF=mAF，求的值．（用含m，n的代数式表示）
（1）中的值为(    )

（上接第4，5题）（3）探究应用：这条道路EF的长为(    )

（上接第4题）（2）类比引申：当∠EAF与∠BAD满足什么关系时，仍有EF=BE+FD？(    )

问题：如图1，点E，F分别在正方形ABCD的边BC，CD上，∠EAF=45°，试判断
BE，EF，FD之间的数量关系．
（1）发现证明：
小聪把△ABE绕点A逆时针旋转90°至△ADG（如图2），经过推理和计算发现BE，EF，FD之间的数量关系，请判断BE，EF，FD之间的数量关系．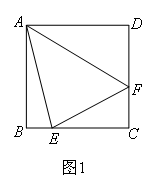

（2）类比引申：
如图3，在四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点E，F分别在边BC，CD上，则当∠EAF与∠BAD满足什么关系时，仍有EF=BE+FD？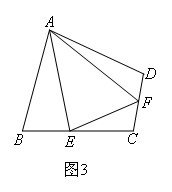

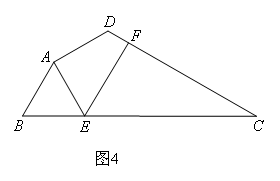
（3）探究应用：
如图4，在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，
∠ADC=120°，∠BAD=150°，道路BC，CD上分别有景点E，F，且AE⊥AD，米，现要在E，F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据：，）．


（建议学生先打印纸质材料，再做题）


（1）中BE，EF，FD之间的数量关系为(    )

（上接第1，2题）（3）对角线AC的长为(    )

（上接第1题）（2）下列说法正确的是(    )