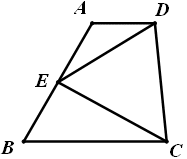
已知在四边形ABCD中,AD∥BC, ∠B=60°,AB=BC,E是AB上的一点,且∠DEC=60°,求证:AD+AE=AB.
答案
连结A、C两点,过点E作EF∥AC,∵∠B=60°,AB=BC,∴△ABC、△EBF均为等边三角形,则∠EFC=120°,BE=BF,∴AE=CF,又∵AD∥BC,所以∠EAD=120°,又∵∠DEC=60°,∴∠FEC+∠AED=60°,又∵∠AED+∠ADE=60°,∴∠FEC=∠ADE,∴△AED≌△FCE(AAS),AD=EF,又∵EF=BE,则AD=BE,由AE+BE=AB知,AE+AD=AB.
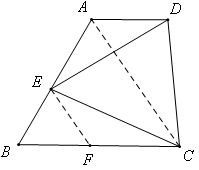
作辅助线,连结A、C两点,过点E作EF∥AC,由于∠B=60°,AB=BC,所以可以知道△ABC、△EBF均为等边三角形,只需证明AD=EF则结论即可证明,由等边三角形的性质,可知∠EFC=120°,BE=BF,所以AE=CF,又因为AD∥BC,所以∠EAD=120°,又因为∠DEC=60°,所以∠FEC+∠AED=60°,又因为∠AED+∠ADE=60°,所以∠FEC=∠ADE,所以△AED≌△FCE(AAS),AD=EF,又因为EF=BE,则AD=BE,由AE+BE=AB知,AE+AD=AB.
不能找到一条合适的辅助线进行有效的解题








