如图，在四边形ABCD中，AB=AD，∠BAD=90°，P是直线CD上一点，连接PA，分别过点B，D作BE⊥PA，DF⊥PA，垂足分别为点E，F．
（1）如图1，当点P在边CD上时，求证：EF=BE-DF．

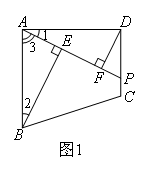
解题思路：
（1）由BE⊥PA，DF⊥PA，得∠DFA=∠AEB=90°，所以∠2+∠3=90°；
又有∠BAD=90°，可以得到∠1+∠3=90°，因此             ，理由是                 ；
又因为AD=BA，∠DFA=∠AEB，因此根据三角形全等的判定定理           ，可以得到△DFA≌△AEB，由全等的性质得到                      ，最后得到EF=AF-AE=BE-DF．
①∠BAE=∠ADF；②∠1=∠2；③同角或等角的余角相等；④同角或等角的补角相等；
⑤AF=BE，DF=AE；⑥∠3=∠ADF，AF=BE；⑦AAS；⑧ASA
以上横线处，依次所填正确的是(    )

• A.①③⑧⑤
• B.②③⑦⑤
• C.②④⑧⑥
• D.①③⑦⑥

答案

正确答案：B

知识点：类比探究  全等三角形的判定和性质  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>