以下是利用平行线的性质来证明三角形内角和等于180°的一种方法，请根据证明过程填空：
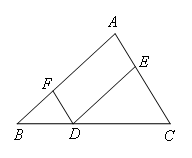
已知：如图，在△ABC中，D为BC上任意一点，过点D作DE∥AB交AC于点E，作DF∥AC交AB于点F．
求证：∠A+∠B+∠C=180°．


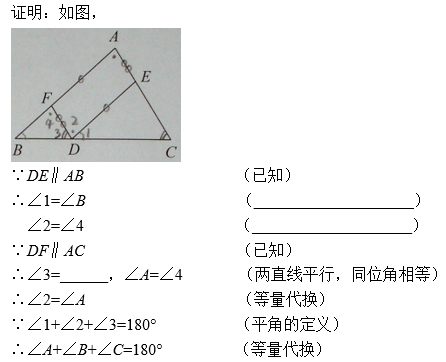
①两直线平行，内错角相等；②两直线平行，同位角相等；③内错角相等，两直线平行；④同位角相等，两直线平行；⑤∠DEC；⑥∠C．
以上空缺处依次所填正确的是(    )

已知DE∥AB，根据两直线平行，同位角相等，得∠1=∠B，
根据两直线平行，内错角相等，得∠2=∠4；
由已知DF∥AC，根据两直线平行，同位角相等，
得∠3=∠C，∠A=∠4，则∠2=∠A；
再根据平角的定义，得∠1+∠2+∠3=180°，
结合∠2=∠A，得到∠A+∠B+∠C=180°．
第一个空：条件是DE∥AB，结论是∠1=∠B，且∠1与∠B是同位角，
因此依据为两直线平行，同位角相等，②正确；
第二个空：条件是DE∥AB，结论是∠2=∠4，且∠2和∠4是内错角，
因此依据为两直线平行，内错角相等，①正确；
第三个空：条件是DF∥AC，结论是∠3=______，而依据是两直线平行，同位角相等，
需要找到∠3的同位角，故应填∠C，⑥正确．
综上所述，②①⑥正确，故选B．

略