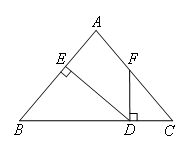
如图，在△ABC中，∠B=∠C，FD⊥BC，DE⊥AB，垂足分别为D，E，
∠AFD=140°，求∠EDF的度数．


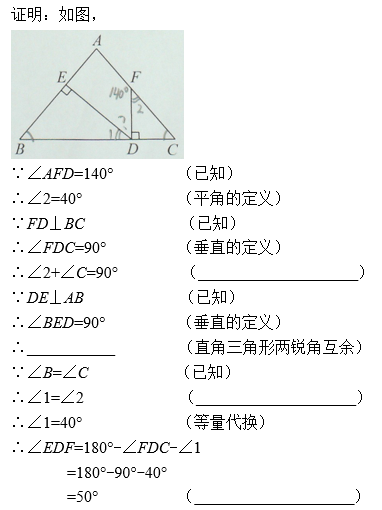
①垂直的定义；②直角三角形两锐角互余；③等角的余角相等；④∠1+∠B=90°；
⑤∠1+∠EDF=90°；⑥平角的定义；⑦三角形的内角和等于180°．
以上空缺处依次所填正确的是(    )

已知FD⊥BC，DE⊥AB，利用垂直的定义，得∠FDC=90°，∠BED=90°，
利用直角三角形两锐角互余，得∠2+∠C=90°，∠1+∠B=90°，
又因为∠B=∠C，利用等角的余角相等，得∠1=∠2，
最后利用平角的定义，得∠EDF=50°．
第一个空：条件是∠FDC=90°，结论是∠2+∠C=90°，
依据是直角三角形两锐角互余，②正确；
第二个空：条件是∠BED=90°，得到结论的依据是直角三角形两锐角互余，
在Rt△BED中，可得∠1+∠B=90°，④正确；
第三个空：条件是∠B=∠C，结论是∠1=∠2，
∠B和∠1互余，∠C和∠2互余，因此依据是等角的余角相等，③正确；
第四个空：条件是∠1=40°，结论是∠EDF=180°-∠FDC-∠1=180°-90°-40°=50°，
∠BDC为平角，因此依据是平角的定义，⑥正确；
综上所述，②④③⑥正确．
故选C．

略