已知：如图，在四边形ABCD中，∠A=62°，∠B=38°，∠BCD=140°，则∠D的度数为(    )

要找到∠D与∠A，∠B，∠BCD之间的关系，
结合图形考虑构造辅助线，把四边形转化为基本图形（三角形），
从而利用三角形内角和定理或三角形外角定理求解．
如图，延长BC交AD于点F，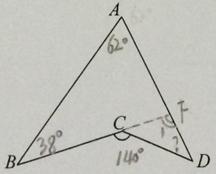

∠1是△ABF的一个外角，结合∠A=62°，∠B=38°，
利用外角定理，得∠1=∠A+∠B=100°；
∠BCD又是△CDF的一个外角，结合∠BCD=140°，
利用外角定理，得∠BCD=∠D+∠1，则∠D=∠BCD-∠1=40°．
本题也可以通过延长DC交AB于点G，或连接AC并延长到H进行计算．
故选A．

略