如图，∠ABC=∠ACB，BD，CD分别平分△ABC的内角∠ABC，外角∠ACP，BE平分外角∠MBC交DC的延长线于点E.以下结论：①∠BDE=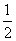∠BAC；②DB⊥BE；③∠BDC+∠ABC=90°；④∠BAC+2∠BEC=180°.其中正确的结论有(    )

①∵∠DCP=∠BDC+∠DBC，2∠DCP=∠BAC+2∠DBC，
∴2(∠BDC+∠DBC)=∠BAC+2∠DBC，
∴∠BDC=∠BAC，故①正确；
②∵BD，BE分别平分△ABC的内角∠ABC，外角∠MBC，
∴∠DBE=∠DBC+∠EBC=∠ABC+∠MBC=×180°=90°，
∴EB⊥DB，故②正确；
③由①知，∠BDC=∠BAC，
∵∠BAC+2∠ABC=180°，
∴∠BAC+∠ABC=90°，
∴∠BDC+∠ABC=90°，故③正确.
④∵∠BEC=180°-(∠MBC+∠NCB)
=180°-(∠BAC+∠ACB+∠BAC+∠ABC)
=180°-(180°+∠BAC)，
∴∠BEC=90°-∠BAC，
∴∠BAC+2∠BEC=180°，故④正确.
故选D

略