(上接第4题)(2)如图2,△ABC是等腰直角三角形,点Q在斜边AB上,以CQ为直角边作等腰直角△PCQ,其中∠PCQ=∠ACB=90°.则AQ,BQ,PQ之间的数量关系为( )

- A.
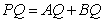
- B.
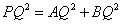
- C.
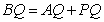
- D.
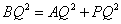
答案
正确答案:B
知识点:略
如图,连接AP,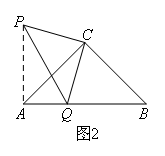
∵△ABC和△CPQ都是等腰直角三角形,∠PCQ=∠ACB=90°,
∴AC=BC,CP=CQ,∠CAB=∠B=45°,
∴∠ACP=∠BCQ,
∴△ACP≌△BCQ(SAS),
∴∠PAC=∠B=45°,AP=BQ,
∴∠PAQ=∠PAC+∠CAB=90°,
在Rt△APQ中,∠PAQ=90°,
由勾股定理得,![]() ,
,
∵AP=BQ,
∴![]() ,
,
故选B.
略








