已知：如图，AB=AC，DB=DC，F是AD的延长线上的一点．
求证：BF=CF．

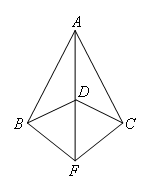
证明：如图，

在△ADB和△ADC中
                         
∴△ADB≌△ADC（     ）
∴                       
在△ABF和△ACF中
                         
∴△ABF≌△ACF（     ）
∴BF=CF
请你仔细观察下列序号所代表的内容：
①；②；③SSS；
④SAS；⑤SSA；⑥∠ABD=∠ACD（全等三角形对应角相等）；
⑦∠1=∠2（全等三角形对应角相等）；⑧；
⑨．
以上空缺处依次填写正确的是(    )

• A.②③⑦⑧④
• B.②③⑥⑨⑤
• C.①④⑦⑧④
• D.①④⑥⑨⑤

答案

正确答案：A

知识点：略  

观察图形，题中已知AB=AC，BD=CD，公共边AD=AD，
由这三个条件可以证得△ADB≌△ADC（SSS）．
再观察图形，对比要证的结论，
可以通过证△ABF≌△ACF得到BF=CF．
由△ADB≌△ADC可得∠1=∠2，
再结合AB=AC，AF=AF（公共边），
由SAS可以证得△ABF≌△ACF，进而可得BF=CF．
空缺处依次所填应为：②③⑦⑧④
故选A．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>