已知:如图,BM平分∠ABC,P为BM上一点,PD⊥BC于点D,BD=AB+CD.
求证:∠BAP+∠BCP=180°.

(截长法)证明:如图,在BC上截取BE=BA,连接PE.

在△ABP和△EBP中

∴△ABP≌△EBP(SAS)
∴
∴CD=ED
∵PD⊥BC
∴∠PDC=∠PDE=90°
在△PCD和△PED中
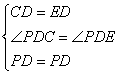
∴△PCD≌△PED(SAS)
请你仔细观察下列序号所代表的内容:
①
 ;
;
②∵∠1=∠2;
③∠A=∠BEP;
④AP=PE;
⑤
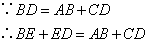 ;
;
⑥
 ;
;
⑦
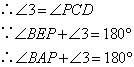 ;
;
⑧
 .
.
以上空缺处依次所填最恰当的是( )
- A.①③⑥⑦
- B.①③⑤⑧
- C.②③⑥⑦
- D.②④⑤⑧
答案
正确答案:B
知识点:略
题中出现BD=AB+CD,这是几条线段间的数量关系,考虑用截长补短转化成两条线段的等量关系.
这里利用截长法证∠BAP+∠BCP=180°,要证△ABP≌△EBP,结合AB=BE,公共边BP,还需要准备∠1=∠2,
第一空应填①;
由全等转移角,可以得到∠A=∠BEP,第二空应填③;
接下来利用三角形全等,证明∠PCD=∠3,结合第一次全等得到的∠A=∠BEP可以得到∠BAP+∠BCP=180°,第三空应填⑤,第四空应填⑧.故选B.
略










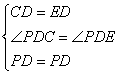
 ;
;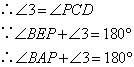 ;
; .
.