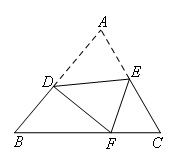
如图，在△ABC中，∠A=70°，∠B=50°，点D，E分别为AB，AC上的点，沿DE折叠，使点A落在BC边上点F处．若△EFC为直角三角形，则∠BDF的度数为(    )

研究△ABC，因为∠A=70°，∠B=50°，所以∠C=60°．
根据轴对称的性质，得∠DFE=∠A=70°．
因为点F是边BC上，所以△EFC为直角三角形，可分两种情况：
①当∠FEC=90°时，如图，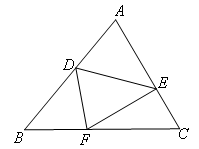

∵∠C=60°，
∴∠EFC=30°
∴∠DFC=100°
∵∠DFC是△BDF的外角
∴∠BDF=∠DFC-∠B
=100°-50°
=50°．
②当∠EFC=90°时，如图，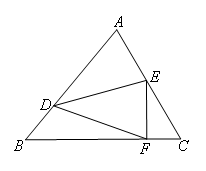

∵∠DFE=70°，
∴∠DFC=160°
∵∠DFC是△BDF的外角
∴∠BDF=∠DFC-∠B
=160°-50°
=110°．
综上，若△EFC为直角三角形，则∠BDF的度数为50°或110°．
故选B

略