在等边三角形ABC所在的平面上有一点P,使得△PBC,△PAC,△PAB都是等腰三角形,则具有该性质的点有( )个.
- A.1
- B.7
- C.10
- D.无数
答案
正确答案:C
知识点:略
因为△PBC,△PAC,△PAB都是等腰三角形,考虑分别以点A,B,C为圆心,AB长为半径作圆,作△ABC三边的垂直平分线.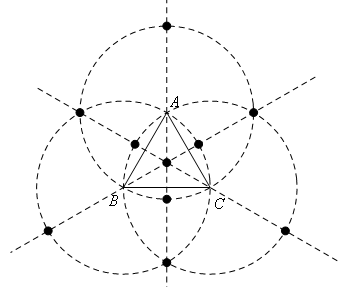
首先找垂直平分线与圆的交点,垂直平分线与垂直平分线的交点,经验证都满足条件,共10个点.再选只在垂直平分线或圆上的点,发现都不满足题意,所以满足条件的点共有10个.
故选C
略



正确答案:C
知识点:略
因为△PBC,△PAC,△PAB都是等腰三角形,考虑分别以点A,B,C为圆心,AB长为半径作圆,作△ABC三边的垂直平分线.
首先找垂直平分线与圆的交点,垂直平分线与垂直平分线的交点,经验证都满足条件,共10个点.再选只在垂直平分线或圆上的点,发现都不满足题意,所以满足条件的点共有10个.
故选C
略
