如图,AB∥CD,AE平分∠CAB,CE平分∠ACD,则∠E=( )
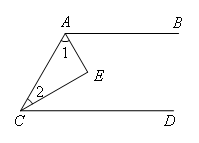
- A.60°
- B.75°
- C.90°
- D.105°
答案
正确答案:C
如图,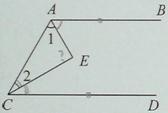
因为AB∥CD,根据两直线平行,同旁内角互补,
可得∠CAB+∠ACD=180°,
因为AE平分∠CAB,CE平分∠ACD,
所以∠1=![]() ∠CAB,∠2=
∠CAB,∠2=![]() ∠ACD,
∠ACD,
∠1+∠2=![]() (∠CAB+∠ACD)=
(∠CAB+∠ACD)=![]() ×180°=90°.
×180°=90°.
在△ACE中,由三角形的内角和等于180°,
可得∠E=180°-(∠1+∠2)=180°-90°=90°.
故选C.
略








