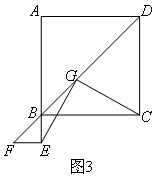
（上接第4，5题）（2）在图1的基础上，将△BEF绕点B逆时针旋转180°，其他条件不变，如图3，为了证明EG和CG之间的数量和位置关系仍成立，类比（1）（2）中的辅助线和证明思路，需要证明两个直角三角形全等，则判断这两个三角形全等时使用的条件是(    )

1．解题要点
照搬（1）（2）中的证明思路：
辅助线（平行夹中点）；
△CBE≌△CDH（EC=HC，∠ECH=90°）；
△ECH是等腰直角三角形．
2．解题过程
如图，延长EG，交AD于点H，连接EC，HC．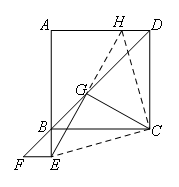

由题意得，F，B，D三点共线，EF∥AD，
∴∠DHG=∠FEG，∠F=∠HDG．
∵FG=DG，
∴△FEG≌△DHG（AAS），
∴DH=EF=BE，EG=HG．
∵BC=DC，∠HDC=∠EBC=90°，
∴△BEC≌△DHC（SAS），
∴EC=HC，∠ECB=∠HCD，
∴∠ECH=∠ECB+∠BCH=∠HCD+∠BCH=90°，
∴△ECH是等腰直角三角形．
∵EG=HG，
∴EG=CG且EG⊥CG，
故证明过程中，判断两个直角三角形全等时使用的条件是SAS．
故选D

略