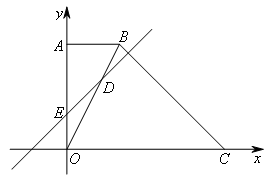
如图,在平面直角坐标系中,直角梯形OABC的边OC,OA分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,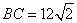 ,点C的坐标为(18,0).若直线DE交梯形对角线BO于点D,交y轴于点E(0,4),点M是直线DE上的一个动点,点N是坐标平面内一点,且四边形OEMN为顶点的四边形是菱形.若点D的横坐标为4,则点N的坐标为( )
,点C的坐标为(18,0).若直线DE交梯形对角线BO于点D,交y轴于点E(0,4),点M是直线DE上的一个动点,点N是坐标平面内一点,且四边形OEMN为顶点的四边形是菱形.若点D的横坐标为4,则点N的坐标为( )
- A.
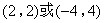
- B.
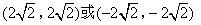
- C.
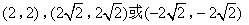
- D.
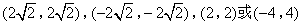
答案
正确答案:B
知识点:略
1.解题要点
若以OEMN为顶点的四边形是菱形,菱形的位置相对固定,
有下面两种情况:
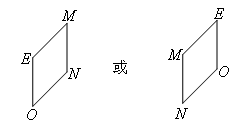
根据菱形的对称性,只需使△OEM为等腰三角形且OE为腰,
点E为顶角顶点即可,然后通过作两条平行线(或沿等腰三角
形底边翻折)找到点N.
2.解题过程
如图,过点B作BF⊥x轴于点F,
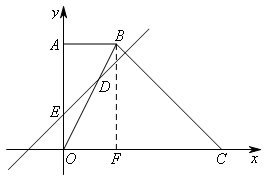
由题意得,点C(18,0),OE=4,
在Rt△BCF中,∠BCO=45°,![]() ,
,
∴BF=CF=12,OF=6
∴B(6,12),A(0,12).
∴![]() ,
,
点D在直线OB上,且点D的横坐标为4,
∴D(4,8),
又E(0,4)
∴![]() .
.
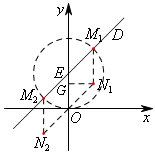
如图,以点E为圆心,OE长为半径作圆,与直线DE交于点
![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,过点O作
,过点O作![]() ,交
,交
![]() 于点
于点![]() ;
;
同理,可作出点![]() ,过点
,过点![]() 作
作![]() 于点G.
于点G.
由题意可得,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
同理,![]() ,
,
∴符合题意的点N的坐标为![]() .
.
故选B
略








