如图,已知A(1,0),B(0,-2),若坐标平面内存在点M,使得△ABM是以AB为腰的等腰直角三角形,则点M的坐标为( )

- A.
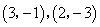
- B.
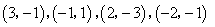
- C.
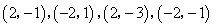
- D.
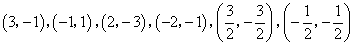
答案
正确答案:B
知识点:略
∵直线y=2x-2与x轴、y轴分别交于A,B两点,
∴B(0,-2),A(1,0).
①当A为直角顶点时,有AB=AM,如图
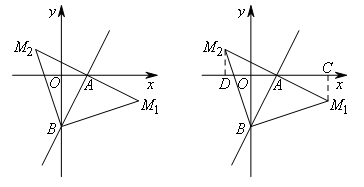
(构造弦图)过点M1作M1C⊥x轴于点C,
则可证△ACM1≌△BOA,
∴AC=BO=2,CM1=OA=1,
∴M1(3,-1);
同理,过点M2作M2D⊥x轴于点D,可证△ADM2≌△BOA,
∴DM2=OA=1,AD=BO=2,
∴OD=1,
∴M2(-1,1);
②当B为直角顶点时,有BA=BM,如图
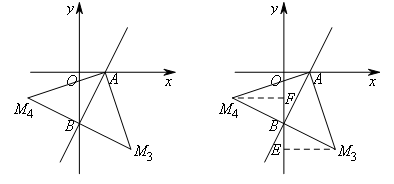
(构造弦图)过点M3作M3E⊥y轴于点E,
则可证△BEM3≌△AOB,
∴BE=AO=1,M3E=OB=2,
∴M3(2,-3);
同理,过点M4作M4F⊥y轴于点F,可证△BFM4≌△AOB,
∴BF=OA=1,M4F=BO=2,
∴OF=1,
∴M4(-2,-1);
③当M为直角顶点时,有MA=MB,此时AB为斜边,不符合题意.
综上,符合题意的点M的坐标为![]() .
.
故选B
略








