如图,∠ACB=90°,∠BAC=30°,△ABD和△ACE都是等边三角形,F为AB的中点,DE交AB于点G,下列结论中:①EF⊥AC;②四边形ADFE是菱形;③AD=4AG;④△DBF≌△EFA,正确的结论是( ) 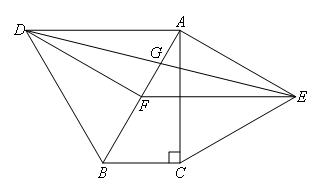
- A.②④
- B.①③
- C.②③④
- D.①③④
答案
正确答案:D
知识点:略

①如图,连接CF,
在Rt△ABC中,∠BAC=30°,F为AB中点,
∴![]() ,
,
又∵△ACE是等边三角形,
∴AE=CE,
又∵EF=EF,
∴△AEF≌△CEF(SSS).
∴∠AEF=∠CEF=![]() =30°,
=30°,
∴EF⊥AC,①正确;
②∵△ABD为等边三角形,且F是AB中点,
∴DF⊥AB,
即在Rt△ADF中,AD是斜边,DF是直角边,
即AD>DF,由此可知四边形ADFE不可能是菱形,②错误;
③由①可知:∠DAB=∠ABC=60°,AC⊥EF,∠ACB=90°,
∴AD∥BC,EF∥BC,
∴AD∥EF,
在Rt△ADF和Rt△AEF中,∠ADF=∠AEF=30°,
∴EF=2AF=AD,
∴四边形ADFE是平行四边形,
∴![]() ,
,
即AD=4AG,③正确;
④由四边形ADFE是平行四边形可得AE=DF,
又∵AD=DB,AD=FE,
∴DB=FE,
又∵AF=FB,
∴△DBF≌△EFA(SSS).
综上,①③④正确.
故选D
略








