如图,直线y=-x+2与x轴、y轴分别交于A,B两点,点P是直线AB上的动点,若使△BOP为等腰三角形,则点P的坐标是( )
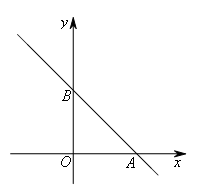
- A.
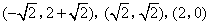
- B.
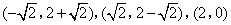
- C.
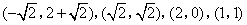
- D.
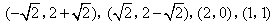
答案
正确答案:D
知识点:略
研究背景图形:
由直线y=-x+2知,B(0,2),A(2,0),∠OAB=45°,
∴∠OBA=45°,
特征:
O,B为定点,P为直线AB上的动点.
定线段OB当腰当底来分类,
当腰时利用两圆来找点,当底时利用一线来找点.
操作:
①如图,当OB为腰时,分别以点O,B为圆心,OB长为半径作圆,与直线AB分别交于点P1,P2,P3,
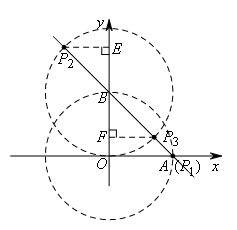
在等腰△BOP1中,OB=OP1,
∴∠OP1B=∠OBP1=45°,
∴点P1与点A重合,
∴P1(2,0),
∵OB=2,
∴BP2=BP3=2,
分别过点P2,P3作P2E⊥y轴于点E,P3F⊥y轴于点F,则
![]()
∴![]()
②如图,当OB为底时,作线段OB的垂直平分线,交直线AB于点P4,交y轴于点M,则
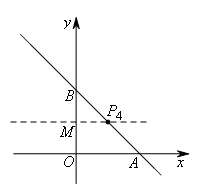
OM=BM=1,
∵∠OBA=45°,
∴MP4=BM=1,
∴P4(1,1)
∴符合题意的点P的坐标为![]()
故选D.
略








