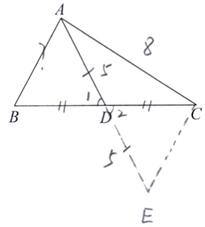
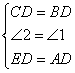已知：如图，在△ABC中，AD为BC边的中线，AD=5，AC=8，求边AB的取值范围．

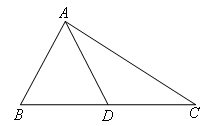
解：如图，                            ．

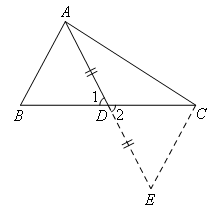
∴AE=2AD
∵AD=5
∴AE=10
∵AD是BC边上的中线
∴BD=CD
在△CDE和△BDA中

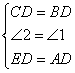
∴△CDE≌△BDA（SAS）
∴                            
在△ACE中，AC=8，
∴10-8 ∴2 请你仔细观察下列序号所代表的内容：
①延长AD到点E，使DE=AD，连接CE；
②延长AD到点E，连接CE；
③延长AD到点E，使DE=AD，连接CE，过点E作CE∥AB；
④CE=BA，∠E=∠BAD；
⑤CE=BA．
以上空缺处依次所填最恰当的是(    )

• A.①⑤
• B.②⑤
• C.③⑥
• D.②⑥

答案

正确答案：A

知识点：三角形全等之倍长中线  

如图，

AD为△ABC的中线，见中线，要倍长，
延长AD到点E，使DE=AD，连接CE；
倍长之后证全等，利用SAS可以证得△CDE≌△BDA；
题中让求边AB的取值范围，所以根据全等三角形对应边相等来转移边，
可得CE=BA；
然后把CE放在△ACE中，利用三角形的三边关系，
可得AE-AC所以2 故选A．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题