已知:如图,在△ABC中,AD是BC边上的中线,分别以AB,AC为直角边向外作等腰直角三角形ABE和等腰直角三角形ACF,连接EF.某同学通过添加辅助线:延长AD到点M,使DM=AD,连接BM.则下列结论错误的是( )
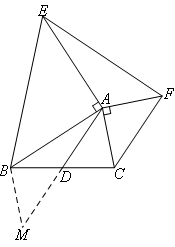
- A.可以利用SAS证明△ADC≌△MDB
- B.AC∥BM
- C.可以利用ASA证明△EAF≌△ABM
- D.EF=2AD
答案
正确答案:C
知识点:三角形全等之倍长中线
见中线要倍长,AD是BC边上中线,延长AD到M,使DM=DA,
然后可以证明△ADC≌△MDB(SAS),由全等转移边、转移角,
得到AC=MB,∠3=∠4,由∠3=∠4可知BM∥AC,
再结合△ABE,△ACF都是等腰直角三角形继续转移条件,
得到△EAF≌△ABM(SAS),进而得到EF=AM=2AD.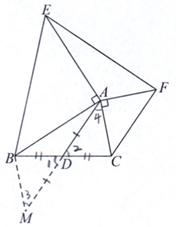
解:如图,
∵AD是△ABC的中线
∴BD=CD
在△ADC和△MDB中
∴△ADC≌△MDB(SAS)
∴AC=MB,∠3=∠4
∴BM∥AC
∴∠ABM+∠BAC=180°
∵△ABE,△ACF都是等腰直角三角形
∴AB=AE,AF=AC,∠BAE=∠CAF=90°
∴∠EAF+∠BAC=180°
∴AF=BM,∠ABM=∠EAF
在△EAF和△ABM中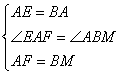
∴△EAF≌△ABM(SAS)
∴EF=AM
∵AD=MD
∴EF=2AD
故选C.
略








