已知△ABC中,AB=AC,点D为直线BC上一动点(不与点B,C重合),以AD为边作△ADF(A,D,F按顺时针排列),使AD=AF,且∠BAC=∠DAF,连接CF.
(1)如图,当点D在边BC上时,求证:BC=CF+CD.
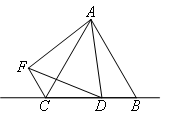
先在图上走通思路后再填写空格内容:
(1)由∠BAC=∠DAF,得∠BAD=∠CAF;又因为AB=AC,AD=AF,因此根据三角形全等的判定 ,可得 ,由全等的性质得 ,所以BC=BD+CD=CF+CD.
请你仔细观察下列序号所代表的内容:
①ASA;②SAS;③SSA;④△ADB≌△AFC;⑤△AFC≌△BAD;⑥△ADB≌△FCD;⑦BD=CF;⑧BD=CF,BC=AC.
以上空缺处依次所填最恰当的是( )
- A.③⑤⑦
- B.②④⑦
- C.③⑤⑧
- D.①⑥⑧
答案
正确答案:B
知识点:三角形全等之类比探究
要证BC=CF+CD,已知BC=BD+CD,只需要证明CF=BD即可,
可以把它们放在两个三角形中证全等.
如图,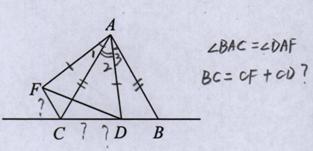
可把本题思路整理成路线图,如图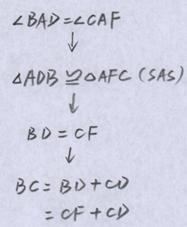
具体过程如下:
∵∠BAC=∠DAF
∴∠2+∠3=∠1+∠2
∴∠3=∠1
在△ADB和△AFC中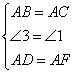
∴△ADB≌△AFC(SAS)
∴BD=CF
∵BC=BD+CD
∴BC=CF+CD
因此空缺处依次所填最恰当的是②④⑦.
故选B.
略








