已知：如图，等边△ABC的边长为8，点D是BC上一点，且BD=6．动点P从点C出发，以每秒2个单位的速度沿CA—AB—BC向终点C运动，连接AD，AP，BP．设点P运动的时间为t秒．解答下列问题：

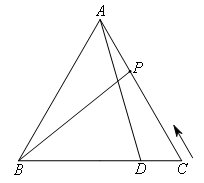
（1）当4≤t≤8时，线段AP的长可用含t的式子表示为(    )

点P速度已知，可判断此题为动点问题，按照动点问题的解决方法解决：
1．研究基本图形，标注：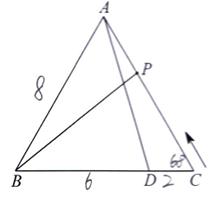

2．研究动点运动状态，包括起点、终点、状态转折点、速度、时间范围，
如图：

3．表达线段长，建等式．
由题意，点P在运动过程中有2个状态转折点，需分成3种情况：
①点P在CA上，对应的时间范围：0≤t≤4；
②点P在AB上，对应的时间范围：4<t≤8；
③点P在BC上，对应的时间范围：8<t≤12．
由题意，当4≤t≤8时，点P在线段AB上运动，如图：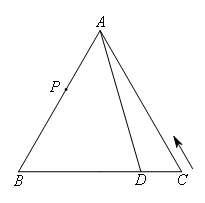

点P已走路程为CA+AP=2t，因此AP=2t-CA=2t-8．
故选C．

略