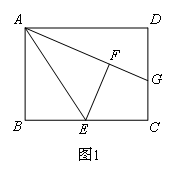
(1)操作发现:如图1,在长方形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在长方形ABCD内部,延长AF交CD于点G.猜想线段GF与GC的数量关系是( )
- A.GF=
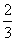 GC
GC - B.GF=GC
- C.GC=
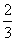 GF
GF - D.GF=2GC
答案
正确答案:B
知识点:略
思路:
①证明两条线段相等,要么放在一个三角形中证等腰,
要么放在两个三角形中证全等;
②观察特征:点E为BC中点,且AB∥CD,符合
“平行+中点”特征;
用思路②进行操作:
如图,延长AE与GC的延长线交于点H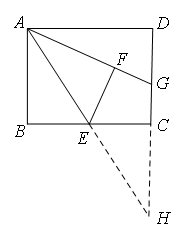
易证:△ABE≌△HCE,
∴∠BAE=∠CHE,AB=HC,
∵△ABE沿AE折叠后得到△AFE,
∴∠BAE=∠FAE,AB=AF,
∴∠CHE=∠FAE,
∴△AHG是等腰三角形,
∴AG=HG,
∴AG-AF=HG-HC
即FG=CG.
故选B
略








