在△ABC中，∠C＞∠B，AE平分∠BAC，F为射线AE上一点（不与点E重合），且FD⊥BC于D．
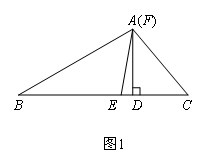
（1）如果点F与点A重合，且∠C=50°，∠B=30°，如图1，求∠EFD的度数．
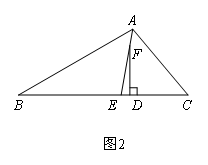
（2）如果点F在线段AE上（不与点A重合），如图2，则∠EFD与∠C-∠B有怎样的数量关系？并说明理由．
（3）如果点F在△ABC外部，（2）中的结论是否仍然成立？若成立，请在图3中画出符合题意的图形并说明理由；若不成立，请直接写出成立的结论．

（1）解：∵∠C=50°，∠B=30°，
∴∠BAC=180°﹣50°﹣30°=100°．
∵AE平分∠BAC，
∴∠BAE=50°．
在△ACE中∠AEC=∠B+∠BAE=80°，
在Rt△ADE中∠EFD=90°﹣80°=10°．
（2）∠EFD=（∠C﹣∠B）
证明：∵AE平分∠BAC，
∴∠BAE==90°﹣（∠C+∠B）
∵∠AEC为△ABE的外角，
∴∠AEC=∠B+90°﹣（∠C+∠B）=90°+（∠B﹣∠C）
∵FD⊥BC，
∴∠FDE=90°．
∴∠EFD=90°﹣90°﹣（∠B﹣∠C）
∴∠EFD=（∠C﹣∠B）
（3）∠EFD=（∠C﹣∠B）．
如图，

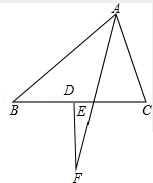
∵AE平分∠BAC，
∴∠BAE=．
∵∠DEF为△ABE的外角，
∴∠DEF=∠B+=90°+（∠B﹣∠C），
∵FD⊥BC，
∴∠FDE=90°．
∴∠EFD=90°﹣90°﹣（∠B﹣∠C）
∴∠EFD=（∠C﹣∠B）．

略