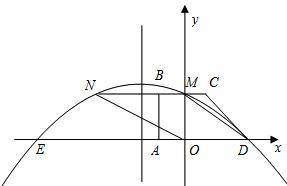
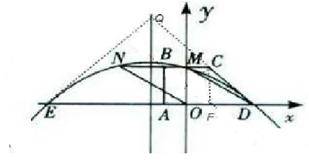
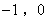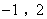四边形ABCD是直角梯形，BC∥AD，∠BAD=90°，BC与y轴相交于点M，且M是BC的中点，A、B、D三点的坐标分别是A（），B（），D（3，0）．连接DM，并把线段DM沿DA方向平移到ON．若抛物线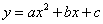经过点D、M、N．设抛物线与x轴的另一个交点为E，点Q是抛物线的对称轴上的一个动点，当点Q在什么位置时有|QE-QC|最大？并求出最大值．

答案

∵BC∥AD，B（-1，2），M是BC与x轴的交点，
∴M（0，2），
∵DM∥ON，D（3，0），
∴N（-3，2），将D（3，0），M（0，2），N（-3，2）代入
解得：y=-x²-x+2；
∴对称轴x=-.
∵M为BC的中点，
∴C（1，2），设直线CD的解析式为y=kx+b，
将C(1,2), D（3，0）：∴y=-x+3
∴当x=-时，y=，故当Q在（-，）的位置时，|QE-QC|=CD最大
.过点C作CF⊥x轴，垂足为F，则CD==.