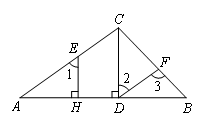
如图，在△ABC中，CD⊥AB，垂足为D，E是AC边上一点，EH⊥AB，垂足为H，∠1=∠2．
（1）试说明DF∥AC；
（2）若∠A=38°，∠BCD=45°，求∠3的度数．

解：（1）∵CD⊥AB，EH⊥AB，
∴∠ADC=∠AHE=90°，
∴CD∥EH，
∴∠1=∠4．
又∵∠1=∠2，
∴∠2=∠4，
∴DF∥AC．
（2）在Rt△ADC中，∵∠A=38°，
∴∠4=180°﹣90°﹣∠A=52°，
∴∠ACB=∠4+∠BCD=97°．
∵DF∥AC，
∴∠3=∠ACB=97°．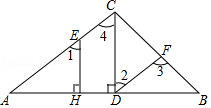

略