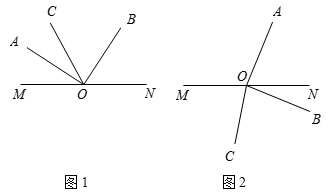
如图1，点O在直线MN上，∠AOB=90°，OC平分∠MOB．
（1）若∠AOC=30°20′，则∠BOC=      ，∠AOM=      ，∠BON=      ；
（2）若∠AOC=α，则∠BON=          ；（用含α的式子表示）
（3）将∠AOB绕着点O顺时针转到图2的位置，其他条件不变，若∠AOC=α（α为钝角），求∠BON的度数．（用含α的式子表示）

（1）∵∠AOB＝90°，∠AOC＝30°20′，
∴∠BOC＝59°40′，
∵OC平分∠MOB，
∴∠BOM＝2∠BOC＝119°20′，
∴∠AOM＝∠BOM﹣∠AOB＝119°20′﹣90°＝29°20′，
∴∠BON＝180°﹣∠BOM＝60°40′
（2）∵∠AOB＝90°，∠AOC＝α，
∴∠BOC＝90°﹣α，
∵OC平分∠MOB，
∴∠BOM＝2∠BOC＝180°﹣2α，
∴∠BON＝180°﹣∠BOM＝2α；
（3）∵∠AOB＝90°，∠AOC＝α，
∴∠BOC＝α﹣90°，
∵OC平分∠MOB，
∴∠MOB＝2∠BOC＝2（α﹣90°）＝2α﹣180°，
∴∠BON＝180°﹣∠MOB＝180°﹣（2α﹣180°）＝360°﹣2α，
故∠BON的度数为360°﹣2α．

略