背景知识：数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律：若数轴上点A、点B表示的数分别为a，b，则A，B两点之间的距离AB=|a-b|，线段AB的中点表示的数为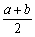
．
问题情境：如图，数轴上点A表示的数为-2，点B表示的数为8，点P从点A出发，以每秒3个单位长度的速度沿数轴向右匀速运动，同时点Q从点B出发，以每秒2个单位长度的速度向左匀速运动．设运动时间为t秒（t＞0）．
综合运用：
（1）填空：①A，B两点间的距离AB= ，线段AB的中点表示的数为 ；
②用含t的代数式表示：t秒后，点P表示的数为 ；点Q表示的数为 ．
（2）求当t为何值时，P，Q两点相遇，并写出相遇点所表示的数．
（3）求当t为何值时，PQ=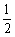
AB．
（4）若点M为PA的中点，点N为PB的中点，点P在运动过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请求出线段MN的长．
．
答案
（1）10；3；-2+3t；8-2t；
（2）当t为2时，P，Q两点相遇，相遇点所表示的数是4；
（3）t为1或3时，PQ=
AB；
（4）不发生变化，MN=5．
解：（1）①A、B两点间的距离AB＝|﹣2﹣8|＝10，
线段AB的中点表示的数为：
＝3．
②t秒后，点P表示的数为-2+3t；点Q表示的数为8-2t；
（2）∵当P、Q两点相遇时，P、Q表示的数相等
∴﹣2+3t＝8﹣2t，
解得：t＝2，
∴当t＝2时，P、Q相遇，
此时，﹣2+3t＝﹣2+3×2＝4，
∴相遇点表示的数为4；
（3）∵t秒后，点P表示的数﹣2+3t，点Q表示的数为8﹣2t，
∴PQ＝|（﹣2+3t）﹣（8﹣2t）|＝|5t﹣10|，
又PQ＝
AB＝×10＝5，
∴|5t﹣10|＝5，
解得：t＝1或3，
∴当t＝1或3时，PQ＝AB；
（4）∵点M表示的数为
＝
﹣2，
点N表示的数为
＝+3，
∴MN＝|（﹣2）﹣（+3）|＝|﹣2﹣﹣3|＝5．
略
WORD格式（
