如图，△ABC是直角三角形，∠ACB=90°，CD⊥AB于D，E是AC的中点，ED的延长线与CB的延长线交于点F.

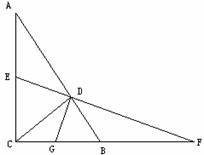
（1）求证：.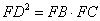
（2）若G是BC的中点，连接GD，GD与EF垂直吗？并说明理由.

答案

（1）证明将结论写成比例的形式，，可以考虑证明△FDB∽△FCD（已经有一个公共角∠F）
Rt△ACD中，E是AC的中点
∴DE=AE
∴∠A=∠ADE
∵∠ADE=∠FDB
∴∠A=∠FDB
而∠A+∠ACD=90°
∠FCD+∠ACD=90°
∴∠A=∠FCD
∴∠FCD=∠FDB
而∠F=∠F
∴△FBD∽△FDC
∴
∴
（2）判断：GD与EF垂直
Rt△CDB中，G是BC的中点，
∴GD＝GB
∴∠GDB=∠GBD
而∠GBD+∠FCD=90°
又∵∠FCD=∠FDB（1的结论）
∴∠GDB+∠FDB=90°
∴GD⊥EF

知识点：相似基本模型应用  

略

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>