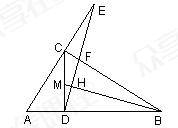
如图，在Rt△ABC中，CD是斜边AB上的高，点M在CD上，DH⊥BM且与AC的延长线交于点E.
求证：（1）△AED∽△CBM；（2）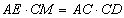

答案

证明：（1）∵∠ACB＝∠ADC＝90°
∴∠A＋∠ACD＝90°
∠BCM＋∠ACD＝90°
∴∠A＝∠BCM
同理可得：∠MDH＝∠MBD
∵∠CMB＝∠CDB＋∠MBD＝90°＋∠MBD
∠ADE＝∠ADC＋∠MDH＝90°＋∠MDH
∴∠ADE＝∠CMB
∴△AED∽△CBM
（2）由上问可知：，
即
故只需证明即可
∵∠A＝∠A，∠ACD＝∠ABC
∴△ACD∽△ABC
∴，即
∴