（1）如图1，等边△ABC中，D为AB边上的动点，以CD为一边，向上作等边△EDC，连结AE，求证：AE//BC
（2）如图2，将（1）中等边△ABC的形状改成为以BC为底边的等腰三角形，所作△EDC改成相似于△ABC，请问：是否仍有AE//BC？证明你的结论.
图1图2

答案

（1）证明：∵∠ACB＝∠ECD
∴∠ACB－∠ACD＝∠ECD－∠ACD，即∠DCB＝∠ECA
在△ECA和△DCB中

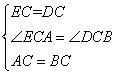
∴△ECA≌△DCB
∴∠EAC＝∠DBC
∴∠EAC＝∠ACB
∴AE//BC
（2）存在
证明：∵△EDC∽△ABC
∴∠ACB＝∠ECD，
∴∠ACB－∠ACD＝∠ECD－∠ACD，即∠DCB＝∠ECA

∴△ECA∽△DCB
∴∠EAC＝∠DBC
∴∠EAC＝∠ACB
∴AE//BC

知识点：相似基本模型应用  

略

略

下载次数：3

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>