如图，在Rt△ABC中，∠ACB=90°，BC=40 cm，AC=30 cm，动点P从点B出发沿射线BA以2 cm/s的速度运动．则当运动时间t=____s时，△BPC为直角三角形．

在Rt△ABC中，∠ACB=90°，BC=40 cm，AC=30 cm，
∴AB==50（cm），
如图，作AB边上的高CD，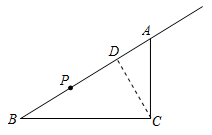

∵，
∴CD=24 cm．
①当∠BCP为直角时，点P与点A重合，
BP=BA=50 cm，
∴t=50÷2=25（s）．
②当∠BPC为直角时，P与D重合，
BP=2tcm，CP=24 cm，BC=40 cm，
在Rt△BCP中，由勾股定理得：
∵，
∴，
解得：t=16．
综上，当t=25或16时，△BPC为直角三角形．
故答案为：25或16．

略