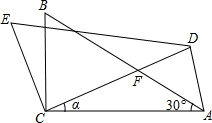
如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,当旋转角α度数为 时,△ADF是等腰三角形.
答案
40°或20°
知识点:弧长、扇形、圆锥、圆柱的相关计算
∵△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,
∴∠DCA=α,CD=CA,
∴∠CDA=∠CAD=(180°-α)=90°-
α,∠BCF=90°-α
∴∠DFA=∠BFC=180°-60°-(90°-α)=30°+α
∠DAF=180°-α-30°-(90°-)=60°-
①当AF=AD时,∠ADF=∠AFD,
即90°-=30°+α,解得α=40°;
②当DF=DA,
∴∠DFA=∠DAF,
∴30°+α=90°--30°,解得α=20°.
③∵∠CDA=90°-,∠DAF=60°-
,∠CDA≠∠DAF
∴DF≠AF
故答案为40°或20°.
略








