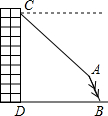
如图，小明站在窗口向外望去，发现楼下有一棵倾斜的大树，在窗口C处测得大树顶部A的俯角为45°，若已知∠ABD=60°，CD=20m，BD=16m，请你帮小明计算一下，如果大树倒在地面上，其顶端A与楼底端D的距离是多少米？（结果保留整数，参考数据：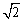
≈1.414，
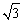≈1.732）．
≈1.414，
≈1.732）．
答案
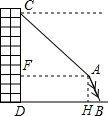
作AF⊥CD于F，AH⊥DB于H，则四边形AFDH为矩形．
∴AF=DH，AH=DF．
由题意可知∠FCA=45°．
∴△CFA为等腰直角三角形
∴AF=CF．
设AB=x米．
在Rt△AHB中，AH=AB·sin60°=
x，
BH=AB•cos60°=
x．
∴AF=DH=DB-BH=（16-x）米．
∴CF=（16-x）米．
又∵CD=CF+FD，
∴20=16-x+x．
解得x≈11．
16-11=5（米）．
∴大树倒下后其顶端A与楼底端D的距离是5米．
知识点：全等三角形的判定与性质 解直角三角形
略
略
WORD格式（
