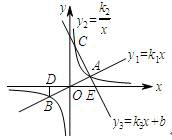
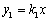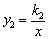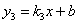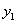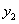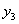如图，正比例函数与反比例函数相交于A、B点，已知点A的坐标为（4，n），BD⊥x轴于点D，且S_△BDO=4.过点A的一次函数与反比例函数的图象交于另一点C，与x轴交于点E（5，0）.（1）求正比例函数、反比例函数和一次函数的解析式；（2）结合图象，求出当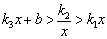时x的取值范围.

答案

（1）∵S_△BDO=4．
∴k₂=2×4=8，
则反比例函数解析式：y₂=.
∵点A（4，n）在反比例函数图象上，
∴，即n=2，
∴点A坐标是（4，2），
∵点A（4，2）在正比例函数y₁=k₁x图象上，
∴2=，即k₁=，
∴正比例函数解析式是：y₁=x.
∵一次函数y₃=k₃x+b过点A（4，2），E（5，0），
∴，解得：
∴一次函数解析式为：y₃=-2x+10.
（2）联立y₃=-2x+10与y₂=，
消去y得：-2x+10=，解得另一交点C的坐标是（1，8），
∵点A（4，2）和点B关于原点中心对称，
∴B（-4，-2），
∴观察图象可得x的取值范围是：x＜-4或1＜x＜4．

知识点：正比例函数的性质  

略

略

下载次数：3

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>