如图，在平面直角坐标系xOy中，已知抛物线顶点N的坐标为（-1．-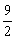
），此抛物线交y轴于B（0，-4），交x轴于A、C两点且A点在C点左边．（1）求抛物线解析式及A、C两点的坐标．
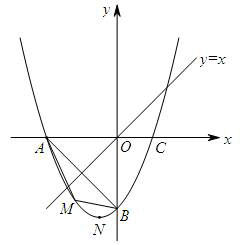
（2）如果点M为第三象限内抛物线上一个动点且它的横坐标为m，设△AMB的面积为S，求S关于m的函数关系式并求出S的最大值．
（3）若点P是抛物线上的动点，点Q是直线y=x上的动点，判断有几个位置使得以点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．
答案
（1）设抛物线解析式为：y=a(x+1)2-
∵抛物线交y轴于B（0，-4）
∴a-=-4，
∴a=
∴抛物线解析式为：y=(x+1)2-或写为y=x2+x-4.
令y=0得：x2+x-4=0，
解得：x1=-4，x2=2
∴A（-4，0），C（2，0）.
（2）
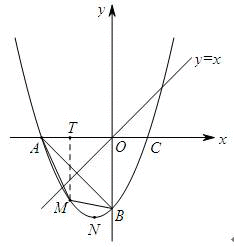
如图，作MT⊥x轴于T，设M（m，n），
则AT=m+4，MT=-n，TO=-m，BO=4．
∴S四边形AMBO=(m+4)(-n)+(-n+4)(-m)=-2m-2n
∵M（m，n）在抛物线上，
∴n=m2+m-4.
∴S四边形AMBO=-2m-2(m2+m-4)=-m2-4m+8.
∵S△AOB=×4×4=8，
∴S=S四边形AMBO-S△AOB=-m2-4m.
∵S为m的二次函数且-1＜0，
∴抛物线开口向下，
∴当m=-2时，S有最大值，最大值为4.
（3）点Q的坐标为（4，4）或（-4，-4）.
略
略
WORD格式（
