已知，△ABC的角平分线BM、CN相交于点P，求证点P到三边AB、AC、BC的距离相等.
答案
作PD、PE、PF分别垂直于三边AB、BC、CA，D、E、F为垂足，
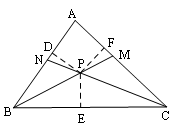
∵BM为△ABC的角平分线，PD⊥AB，PE⊥BC，
∴PD=PE（角平分线上的点到这个角两边的距离相等）．
同理可证：PF=PE．
∴PD=PE=PF．
即点P到三边AB、BC、CA的距离相等．
知识点：角平分线的性质
作PD、PE、PF分别垂直于三边AB、BC、CA，D、E、F为垂足，根据角平分线性质可得PD=PE，PF=PE，所以PD=PE=PF．
对角平分线的性质掌握不牢
WORD格式（
